济南雕刻机的差分插补理论

相信大家都清楚，济南雕刻机发挥作用，主要是靠其内部的系统程序来进行的，而且别看这小小的雕刻机，它的内部系统程序是很复杂的，涉及到的方面非常多，涉及到的理论也非常多，下面木工雕刻机厂家--友达数控就雕刻机的差分插补理论为大家简单介绍一下，大家可以好好了解一下，对于雕刻机的运行也会有更加清晰的认识。

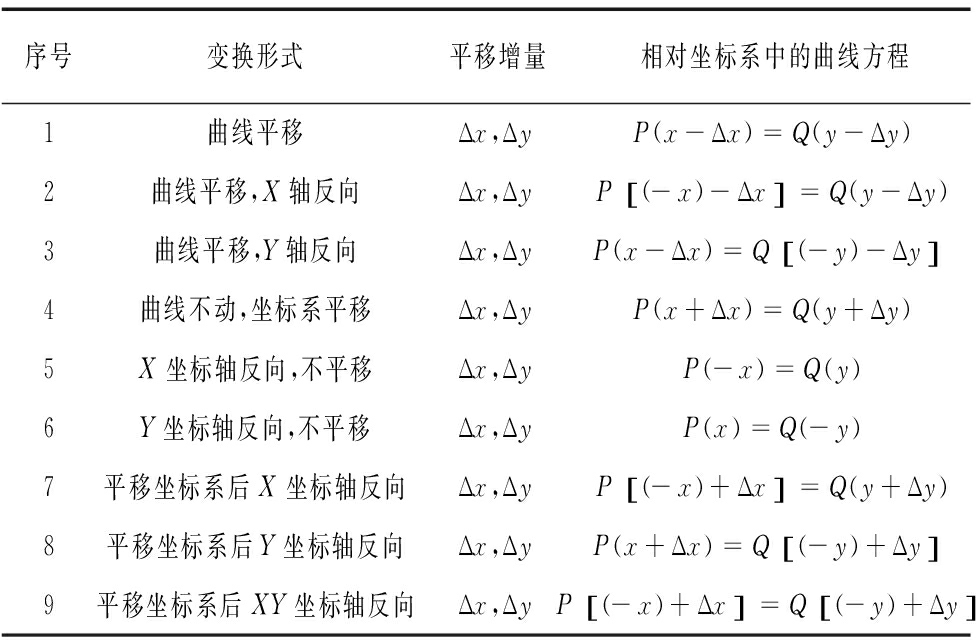
1.曲线方程平移变换

济南雕刻机的差分插补理论要求将绝对坐标系中的曲线转化到相对坐标系第一象限内，即当曲线在插补过程中越过第一象限的时候，要将曲线经变换转化到第一象限中去。设绝对坐标系中的曲线方程为P(x)=Q(y)，经表中的平移变换即可转化到相对坐标系中。

2.差分插补理论框图

木工雕刻机厂家以函数P(x)=axm(m为正整数)为例进行差分递推，第一个差分点为x=0，步长为1(下文中用jxim表示Pm(x)在xi的第m阶差分)。计算出各离散点的P(x)值后，由差分定义，可逐步的求出各点处的各阶差分和函数值，即：

P(xi)=P(xi-1)+jxi-11

式中:

jxi-11=jxi-21+jxi-22

设正高次曲线的方程为Pm(x)=Qn(y)，该式中：

Pm(x)=amxm+am-1xm-1+……+a1x1

Qn(y)=bnyn+bn-1yn-1+……+b1y1

求出Pm(x)在x=0处的1～m阶差分和Qn(y)在y=0处的1～n阶差分，以曲线加工起点为原点，使起点处的切线位于相对坐标系的第一象限内，此时Pm(x)和Qn(y)在起点处的值都为0。每当X轴或Y轴进给一步，相应坐标点处的Pm(x)或Qn(y)值都要加上该点的一阶差分值，并且在进给过程中要尽量保持Pm(x)=Qn(y)，差分插补理论的程序框图如图所示。

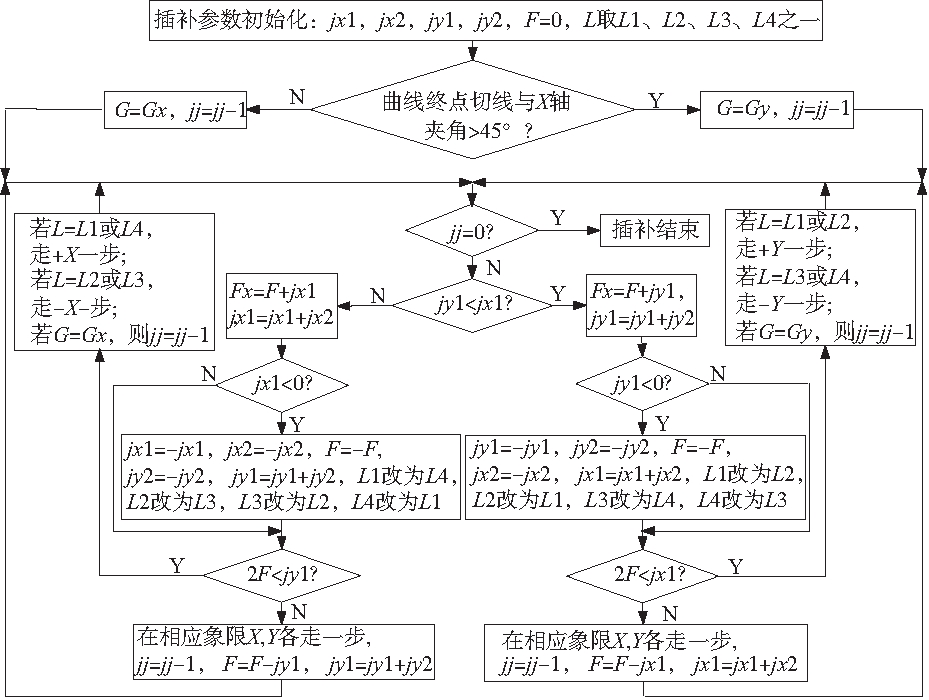
在保持F=Pm(x)-Qn(y)最小的原则下，优先插补一阶差分值(jx1或jy1)较小的坐标轴，X轴和Y轴可单独进给，也可联动。当jx1<0或jy1<0时，就表示曲线越过了象限,要进行过象限处理：

当jx1<0时，进行过象限处理：jx1=-jx1，jx2=-jx2，jy2=-jy2，jy1=jy1+jy2，F=-F。当jy1<0时，进行过象限处理：jy1=-jy1，jy2=-jy2，jx2=-jx2，jx1=jx1+jx2，F=-F。图1中各参数含义：jx1，jx2表示Pm(x)的一阶和二阶差分。jy1，jy2表示Qn(y)的一阶和二阶差分。L1，L2，L3，L4表示绝对坐标系中的四个象限。L表示绝对坐标系中，当前插补位置的象限号。G表示计数方向，G=Gx时取X轴方向，G=Gy时取Y轴方向。jj表示插补计数次数。当G取X轴方向时，jj是曲线在X轴投影长度叠加之和。当G取Y轴方向时，jj是曲线在Y轴投影长度叠加之和。图中的L1改为L4表示L由取L1改为L取L4，以此类推。

以上内容便是友达数控为大家介绍的济南雕刻机的差分插补理论的相关内容，可以看出，是比较复杂的，但是大家不要惊讶，雕刻机的内部系统也是博大精深的，这只能算是雕刻机内部系统中的一小部分，而雕刻机的“自动化”是由很多像这样的程序共同完成的。

相关文章： 济南雕刻机 木工雕刻机厂家